
 |
 Algunos
sabrán, (la mayoría no lo sabe), que tanto en forma aérea como naval,
Algunos
sabrán, (la mayoría no lo sabe), que tanto en forma aérea como naval,
existen dos formas de
trazar rutas en cuanto a largas distancias se trata.
Muchos, se preguntarán
sobre el por qué de estas variantes,
de las cuales se pueden resumir con las siguientes frases:
"QUE SEA LA MÁS CORTA, AUNQUE RESULTE MÁS COMPLICADA
DE EFECTUAR"
"QUE SEA FÁCIL DE EFECTUAR, AUNQUE NO SEA LA MÁS CORTA"
(Preferentemente, ver en ordenador. Aún no adaptada a celular)
El desarrollo de este tema, será por demás extenso. Por ello, consideré necesario implementar un índice:
|
El índice de lo que aquí se verá. |
|
|
Dada la extensión de esta web, resumo
en pocas líneas su contenido:
Identificadas estos tipo de trazas/rutas, hablo sobre ellas, cómo identificarlas debidamente y cómo diferenciarlas; ampliando más sobre cómo son cada una. Ya, cuando uno cree que al menos se posee una base importante sobre ellas, identifico las confusiones que, aunque parezca mentira ante su análisis fino, pueden llegar a sufrirse. Uno que otro ejemplo en relación de "estas confusiones" en donde muy probablemente se requiera "comenzar a leer nuevamente, ya que hemos quedado insertos en una IMPENSABLE PARADOJA! |
|
I M P O R T A N T
E |
1.- Introducción:
|
Pongámonos
en escena: Ya sea en avión o en barco, supongamos que requerimos efectuar una gran distancia entre dos puntos. Para ser más específicos, digamos que queremos ir de un continente al otro.
Pensar en ello, nos resulta por demás sencillo ya que nuestro primer
pensamiento será
"sigo derechito
y ya!",
(cosa que es más que correcto), en donde intuitivamente, para trazarlo,
tomaríamos un mapa tipo
Mercator, trazaríamos una línea recta
entre ambos puntos, mediríamos los grados de rumbo y ya tendríamos todo
resuelto. |
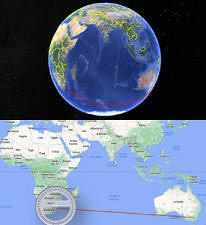 Vemos cómo la traza de una misma ruta, es por demás distinta dependiendo en dónde la tracemos. |
 Ahora bien, si al mismo tiempo, hacemos lo mismo pero en un globo terráqueo de escritorio, ¿Cómo marcaríamos ese trazo? Pareciera una acción simple, pero es medio complicadita en la práctica.. |
|
|
Al comparar
visualmente ambas marcas... NO SON LAS MISMAS!...
Siempre
dependerá de cómo la hemos marcado en nuestro globo terráqueo y si esa
forma fue la correcta!. |
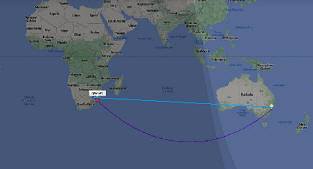 |
|
He aquí, la traza efectuada en
nuestro Mercator, (celeste) y si proyectáramos en este mapa lo ya marcado
en nuestro globo terráqueo. |
|
 Debemos
ser conscientes que al momento de llevar a la práctica un viaje de tal
magnitud, (y más si consideramos que cruzaremos un océano), no nos
guiaremos por el paisaje y otras referencias geográficas visuales, (como
ser ciertas ciudades, montañas, lagos, etc); sino que debemos efectuar tal
trayecto, utilizando para guiarnos, el instrumental que al caso corresponda;
ante la consigna que:
"debemos seguir
cierto rumbo" para lograrlo. Debemos
ser conscientes que al momento de llevar a la práctica un viaje de tal
magnitud, (y más si consideramos que cruzaremos un océano), no nos
guiaremos por el paisaje y otras referencias geográficas visuales, (como
ser ciertas ciudades, montañas, lagos, etc); sino que debemos efectuar tal
trayecto, utilizando para guiarnos, el instrumental que al caso corresponda;
ante la consigna que:
"debemos seguir
cierto rumbo" para lograrlo.(Valen las comillas). |
|
|
NO TOMARÍAMOS EN CUENTA y es que debemos considerar que no sólo nuestro mundo es esférico sino que los puntos de coordenadas terrestres están determinados por paralelos y meridianos; siendo que los primeros "son paralelos entre sí" (valga la redundancia) y los segundos no lo son. Pero tomemos esto último con pinzas así no nos complicamos desde un principio ya que, a posterior, nos quedará claro. |
|
|
ALGO MUY IMPORTANTE |
|
Cuando
hablamos de una
Puede
parecer una tontera, pero cuando avancemos en el tema, A TOMARLO EN CUENTA!
|
|
NOTA: |
|
Quienes ya conozcan estos términos y diferencien uno de otro; pero sí están
interesados en saber por qué titulé a esta aplicación como
"PARADOJA", |
Diagramemos nuestro viaje...
|
Acabamos de
notar que no es lo mismo marcar una ruta en un mapa "estándar" que en un
globo terráqueo de escritorio... ¿Eso implica que una de las dos trazas es incorrecta? NO! Ambas trazas son correctas aunque en apariencia son distintas por más que ambas cumplan su objetivo; pero ahora nos generaría la duda sobre cuál de ambas rutas es la más óptima para el caso. Entonces... ¿Qué ruta debo "trazar" y CÓMO hacerlo correctamente? Si nos tomáramos el trabajo de medir en escala ambos trazos, notaremos que sus distancias NO SON EXACTAMENTE IGUALES y que de hecho, NO COINCIDEN PARA NADA EN CUANTO AL RUMBO A TOMAR, en donde una traza mantiene un rumbo exacto y que la otra VARÍA CONSTANTEMENTE! Tal, lo dicho al principio, pueden surgir dos variantes bien concretas: ¿Recuerdan lo que inicialmente nos autocuestionamos? |
|
|
"QUE SEA LA MÁS CORTA, AUNQUE RESULTE MÁS COMPLICADA DE EFECTUAR" |
Así es, aunque hasta el momento no lleguemos a entender sobre ambas variantes tan dispares; hemos notado que:
|
Si sencillamente en un mapa trazamos una línea recta entre ambos puntos, todo indicaría que seguimos un único rumbo y que no nos resultaría complicado hacerlo en la práctica. A esta ruta, se le llama LOXODRÓMICA. |
|
|
|
Si en forma un poco complicada, intentamos marcar una ruta más extensa, pero sobre un globo terráqueo, intentando hacerla lo más directa posible; veremos que cruzando a los paralelos y meridianos, como que no se mantiene un rumbo fijo!... Aún, sobre cómo llevarlo a la práctica, no tenemos la menor idea de cómo lo lograremos!!!. Ya veremos! A esta ruta, se le llama ORTODRÓMICA. |
Para COMENZAR a entenderlo, primero conozcamos a ambas, pero enunciando sus pro y sus contras:
| RUTA LOXODRÓMICA: | No es la más corta, pero con sólo seguir UN RUMBO, llegaremos al destino. |
| RUTA ORTODRÓMICA: | La más corta posible, pero no es tan sencillo llevarla a cabo. |
Ahora sí,
ampliemos más información sobre estas dos tipos de navegación:
2.- Resumen de definiciones:
|
Vayamos a lo
que sería una definición medianamente simple, resumida y con sus
comparativas, entre ortodrómica y loxodrómica, tal como podremos
encontrarlo en internet. (Si tenés dudas en cuanto a cuan ovoide oblato o esférico es nuestro planeta, observa esta imagen). |
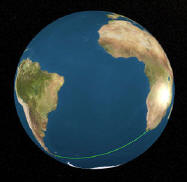 |
RUTA
ORTODRÓMICA:
La navegación
ortodrómica (del
griego ὀρθός ‘recto’
y δρόμος ‘carrera’)
o navegación por el círculo máximo, es la que sigue
la distancia más corta entre dos puntos,
es decir, es la que sigue |
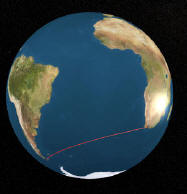 |
RUTA LOXODRÓMICA: La navegación loxodrómica alude a la loxodromia (del griego λοξóς -oblicuo- y δρóμος -carrera, curso-), es decir a la curva que sobre la superficie de la Tierra constituye un mismo ángulo al hacer intersecar todos los meridianos sirviendo de este modo para mantener un rumbo constante al navegar.
Interprétese: |
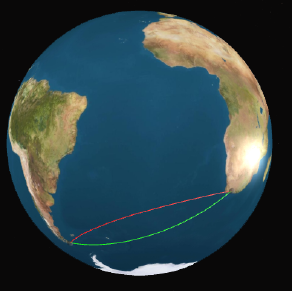 AQUÍ PODEMOS VER A AMBAS TRAZAS. Parecieran similares... pero obviamente no lo son. |
|
¿Vieron que en lo recientemente explicado, sobresalen las palabras
CURVA
Y
RECTA?
CUIDADO CON ESO!
No nos olvidemos de ésto!

_____________
|
|
|
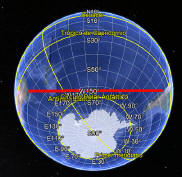 |
Así, se ve la misma traza
ortodrómica en una esfera DESDE SU VISTA SUPERIOR, observando que ésta es una recta perfecta. |
|
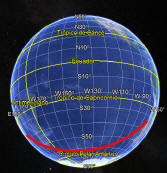 |
La misma traza ortodrómica en
una esfera, pero vista con cierta inclinación. Lógicamente trayecto RECTO, pareciera ser una muy prolongada curva. Pero, claro! Hablamos de una ruta/trayecto, pegada en una superficie esférica en cuanto a su horizontal corresponde. |
|
|
|
Ahora bien. Cuando transportamos dicha ruta ortodrómica a una proyección tipo Mercator, (de esférico 3D a plano 2D), la misma queda representada como una gran curva. Pero
insisto. |
|
EN LA TRAZA ORTODRÓMICA
Es aquí en
donde nuevamente |
|
|
|
LA TRAYECTORIA es recta. (2D) VISTA SUPERIOR |
El RECORRIDO es curvo. (3D) VISTA LATERAL |
|
Sigamos:
A fin que no
queden dudas, hemos visto que en lo que respecta a ortodrómicas, se hace mención
del
CÍRCULO MÁXIMO.
Veamos a qué nos referimos con esto:
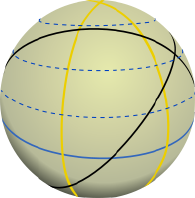 |
Por definición,
El gran círculo, denominado también círculo
mayor o círculo máximo,
es el círculo resultante de una sección realizada
a una esfera mediante un plano que pase por su centro y la divida en dos
hemisferios; la sección circular obtenida tiene el mismo diámetro que la
esfera. En consecuencia, deducimos que la línea del ecuador es un CÍRCULO MÁXIMO como también lo son los infinitos meridianos que fueron trazados en nuestro planeta. No pasa lo mismo con los paralelos, (salvo el Ecuador como ya se ha dicho), siendo éstos círculos mínimos que, ante una división de partes, formaría el perímetro de la base de un casquete sin llegar a ser una media esfera. |
3.- Interpretación simple de cada una:
NO DESESPEREN!
Puede parecer muy complicado, pero no lo es tanto.
Comencemos:
|
ORTODRÓMICA: |
|
|
Ya hemos visto que
la misma es un arco de un círculo máximo de una esfera y que es la recta más
corta posible; pero no pretendo meterme en campo geométrico sino que al menos se
entienda su concepto en forma por demás casera. Observando en esta imagen, notamos que la intercepción de dicha traza con los meridianos, sus ángulos conformados no son iguales en absoluto; viendo también que la traza comienza con un rumbo noreste y que concluye con un rumbo sudeste.
|
|
|
Visualmente, no tendremos duda alguna que es la distancia más corta posible entre estos puntos y que su trayecto (en vista superior) es una recta perfecta! RECORDAR!: No confundir "recta por vista superior" con la curva que se verá "lateralmente" ya que se sigue en paralelo con la curvatura terrestre. En el caso de haber utilizado un globo terráqueo y tal lo antes dicho, veremos también que el ángulo que se forma entre meridianos y paralelos, NO SON LOS MISMOS EN DISTINTOS PUNTOS DE SU TRAYECTO. |
 |
|
LOXODROMICA: |
|
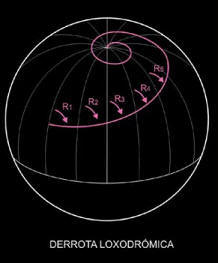 ¿Y
en el caso de una ruta loxodrómica? ¿Y
en el caso de una ruta loxodrómica?
Para explicar
más simplemente este tipo de ruta, haremos al revés. Como ya lo hemos
dicho antes, nos guiaremos en base a un mapa tipo Mercator (como los que
veíamos en la Escuela). LISTO!...
Pero... Algo
importante a considerar: |
|
 Para
adelantarnos al tema, si consideramos que viendo nuestro Mercator, el
norte es 0°; hacia la derecha nuestra, (este), es 90°; hacia abajo es 180°
y nuestra izquierda es 270°, con el solo hecho de tomar un transportador y
medir los grados de nuestro trazo, Para
adelantarnos al tema, si consideramos que viendo nuestro Mercator, el
norte es 0°; hacia la derecha nuestra, (este), es 90°; hacia abajo es 180°
y nuestra izquierda es 270°, con el solo hecho de tomar un transportador y
medir los grados de nuestro trazo, |
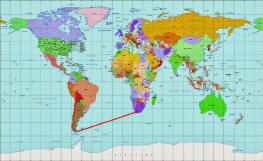 |
YA TENDREMOS NUESTRO CURSO FIJO A SEGUIR! |
|
Antes de
concluir esta etapa, razonemos lo siguiente aunque al hacerlo generaremos una
pequeña confusión entre concepto y definiciones puras:
Una navegación por el Ecuador terrestre es lógicamente una ORTODRÓMICA ya que
tomamos un arco de un círculo máximo terrestre.
Peeero, viendo que para hacerlo
mantenemos un mismo
rumbo,
PODRÍAMOS DECIR QUE TAMBIÉN ES UNA RUTA LOXODRÓMICA aunque no coincida con su
definición pura.
Algo similar pasa si navegamos por cualquiera de los meridianos, en donde respetando "mantener" el rumbo 0° o 180°, lo podemos tomar como una ruta LOXODRÓMICA, pero también éste forma parte de un círculo máximo siendo una ruta ORTODRÓMICA y en donde inevitablemente también su proyección pasaría por los polos.
4.- Esfera (3D) Vs. Mapa (2D).
|
La realidad
inequívoca de nuestro mundo, no es ni nada más ni nada menos que lo que a
escala nos muestra, UN GLOBO TERRÁQUEO. Sin ninguna duda, resulta por demás impráctico "para la cartera de la dama y el bolsillo del caballero", andar con uno de éstos encima y ni qué hablar de llevar a uno de estos en la cabina de un avión con la escala visual que se requeriría. (Lógico. Ahora la informática, nos lo permite). Métodos de trazados, copias de los mismos, sería por demás tedioso en todo concepto; recordando que el inicio histórico de los levantamientos topográficos han comenzado por secciones pequeñas y ampliándose a medida que la humanidad iba conociendo mayor territorio; plasmándose ésta sobre superficies planas. |
 |
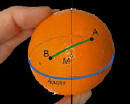
| No resulta en vano recordar que nuestro planeta es enorme, cuyo perímetro de la Tierra es de 40.075 km. y en donde por lógica, la redondez terrestre a escala visual es inapreciable, considerando que la cuerda de un arco de circunferencia terrestre decae sólo 1° cada 111 km. | |
 |
Así es! Un
cuerpo geométrico (3D), es literal como para relacionar lugares y
distancias a UNA GRAN ESCALA, en donde deberíamos tener una gran cantidad
de "gajos parciales en tres dimensiones de una esfera" para tener
ampliada cada zona en particular; pero por demás impráctico para cortas y
medianas distancias en donde muy poca sería la diferencia con su
proyección plana. Sin duda alguna y ante la practicidad que se requiere y pretende, la utilización de mapas en papel (2D) de tipo "proyección", nos soluciona todos los problemas y más aún en cuanto a una escala deseada. |
|
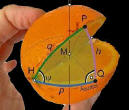
Ahora bien. ¿Es posible plasmar en forma literal en un papel plano un cuerpo geométrico? Desde luego que no!... Se cae de maduro que una figura 3D es incompatible con algo en dos dimensiones en lo que respecta a equidad visual. A lo sumo, si por ejemplo quisiésemos plasmar una pequeña zona, considerando el gran diámetro terrestre, sí podríamos decir que esa representación en mapa sería "casi" exacta; pero jamás se podrá hacer en grandes extensiones. Por ello, cual cáscara de naranja que se separa en gajos y que se aplastan para estos ser aplanados, se generará una "deformación" de esta superficie. |
 |
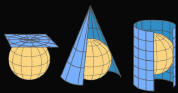 |
A este método
de convertir la superficie de una figura geométrica en una superficie
plana, en lo que a cartografía se refiere, se le denomina "PROYECCIÓN". Existen distintos tipos de proyecciones diversas de las cuales cada una se aplicará a un requerimiento en particular; pero a sabiendas que tal lo dicho, su reflejo generará distintos tipos de deformaciones dependiendo de cómo es dicha proyección. No obstante, con el conocimiento de ésta y con los cálculos que se requieran, será por demás preciso todo cálculo a plasmar con ellas. |
|
CONCLUSIÓN: |
|
|
|
|
|
Una ortodrómica
en un globo
es
una recta;........................................y
sin embargo, en un Mercator
SE VE CURVA!!! |
¿Esta sería
la PARADOJA que anuncia el título?
No. Aún no llegamos a eso.
5.- Resumen parcial
Resumamos hasta
ahora...
Ante la elección de tipo de ruta a efectuar, nos han quedado dos opciones:

|
1ra. opción.
|
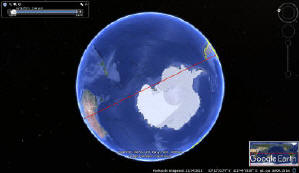 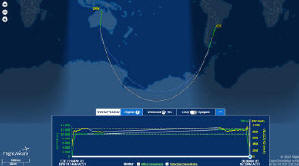 Aquí, el vuelo QAF14 en sus dos vistas:
|
|
Ejemplo de
la programación de una ruta aérea ortodrómica: |
|
Pero, ¿es complicado conocer la ruta ortodrómica entre dos puntos? |
|
|
|
Ahora bien.
|
|
A- Buenos Aires: Ezeiza Latitud: 34° 48.48´ S Longitud: 58° 32.19´W B- Miami: Latitud: 25° 47.43´ N Longitud: 80° 17.19´W Coseno C = Cos A * Cos B + Sen A * Sen B * Cos C Coseno C = Coseno (90+34) * Cos (90-25) + Sen (90+34) * Sen (90-25) * Cos (Incremento de Longitud) Incremento: 80° 17.19´ 58° 32.19´ ----------- 21° 45´ Coseno C = Coseno (124° 48.48´) * Cos (64° 12.57´) + Sen (124° 48.48´) * Sen (64° 12.57´) * Cos (21° 45´) Coseno C = Coseno (124.8) * Cos (64.29) + Sen (124.8) * Sen (64.29) * Cos (21.75) Coseno C = -0.57 * 0.43 + 0.82 * 0.90 * 0.93 Coseno C = -0.2451 + 0.68634 = 0.44124 C = ArcoCoseno (0.44124) = 63.81697 ° 360 grados son 40.008 km 63.81697 son X X = 7092 km (4406 MN) |
|

|
2da. opción. LOXODRÓMICA A la hora de la decisión, nos resultará mucho más sencillo marcar en un mapa Mercator, un trazo RECTO desde nuestro punto de salida hacia nuestro destino; medir en él con un simple transportador el rumbo a seguir y ya, en viaje, mantener siempre dicho rumbo fijo. Hemos visto que si bien lo hemos trazado RECTO, en la realidad práctica estaremos haciendo una gran curva a modo espiral, pero que éste no será físicamente notorio ya que lo único que debemos hacer es "clavar" nuestra brújula con el rumbo que corresponde. Eso sí. No será el camino más corto. FÁCIL! (Pero impráctico en tiempo y costos).
|
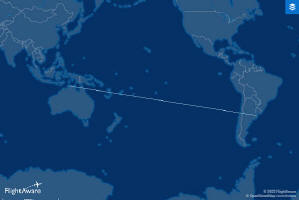
|
|
|
|
¿Los confundió esta imagen? |
Sigamos...
Para los ejemplos
citados en ambas opciones, hemos utilizado el vuelo QAF14 que partió de EZE
(Buenos Aires, Rep. Argentina), con destino a DRW (Darwin, Australia).
Fuente:
https://www.flightaware.com/live/flight/QFA14
(Para más
detalles sobre este vuelo y otros similares, dirigirse a:
LA ANTÁRTIDA, AUSTRALIA Y LOS VUELOS).
Sin considerar cualquier cambio se rumbo fuera de lo normal o por meteorología, (es decir, considerando sólo ambas rutas en su aspecto geométrico puro), he aquí las diferencias en distancia y duración de vuelo e ambas opciones y nótese también los rumbos iniciales de cada una de ellas:
|
|
Peeero...
Luego de este análisis, no ha quedado en mente una pequeña ensalada entre los
términos
"RECTO" y "CURVA"
y entre
"LO GRAFICADO"
y
lo que:
"REALMENTE HARÉ EN VIAJE"...
En parte,
SUENA A CONTRADICTORIO!
(Tranquilos... Tampoco es la paradoja enunciada).
No obstante, analizando conscientemente lo escrito hasta aquí y graficándonos con algo esférico, no tardaremos mucho en interpretarlo PARA SIEMPRE, salvo que...
SE NOS HAYA GENERADO OTRA INCÓGNITA!
Ya sea haciéndolo en forma física o mental, al intentar plasmar una ruta
ortodrómica,
VEO QUE LA RUTA ORTODRÓMICA NO ES RECTA TAL LO DICHO SINO QUE ESTÁ SIGUIENDO LA
CURVATURA TERRESTRE!
¡UNA ORTODRÓMICA ES CURVA!!!
"Cuando aprendimos las respuestas nos cambiaron las preguntas"...
Aquí, es cuando ya hasta ponemos dudas hasta sobre la definición pura de
ORTODRÓMICA = ORTO => RECTO.
Por ello, analicemos lo siguiente:
6.- Curso - rumbo - trayectoria
 No
pretendo aquí
explayarme en conceptos técnicos de navegación
No
pretendo aquí
explayarme en conceptos técnicos de navegación
y llegar a explicar las diferencias entre "curso - rumbo - derrota"
ya que ello está muy ligado a lo práctico y lo meteorológico (que no
incluimos aquí);
pero al menos
INTERPRETEMOS que el RUMBO A SEGUIR
es lo que una hipotética brújula nos indicará y que ello debemos respetar.
Pero...
|
Considero que,
ante el caso que estamos tratando, (y sólo para este caso),
"RUMBO / CURSO"
"LA TRAYECTORIA DEL TRAZO"
Normalmente, podemos interpretar que cuando uno dice RUMBO, puede estar indicando algo como:
"Rumbo noreste" o bien, "rumbo 045°".
En este caso, para no generar confusiones y sólo para que quede claro" y diferenciarlo del rumbo, definamos al CURSO cual reyes magos apuntando con su dedo hacia la estrella de Belén como si se dijera:
Soy consciente
que esto puede resultar confuso para muchos y que sin dudas pareciera que hasta contradice a un libro de navegación, pero considero que "con
peras y manzanas" podrá ser más entendible que aplicando tecnicismos y más
aún ante la explicación de este tipos de rutas. (Recordando que estamos
hilando demasiado fino)...
|
|
Y VUEEEELVO A REITERAR!!! |
|
En lo que
respecta a las definiciones de |
|
|
Sí... Soy insistente con lo mismo...
Pero "por algo" lo reitero tanto...

7.- Aunque pareciera tonto...
Previo a meternos en "LA PARADOJA", consideré necesario lo siguiente:
Lo que a continuación expondré, será motivo suficiente para que cualquiera que lo lea, se sienta ofendido como si yo pensara que me estoy dirigiendo hacia personas tontas; pero aunque parezca mentira, es importante al menos hacer mención sobre esto; porque a la hora de hacer comparaciones imaginarias, nuestra mente nos puede hacer una mala jugada al dibujar en nuestro cerebro ciertas escenas a fin de recrearlas.
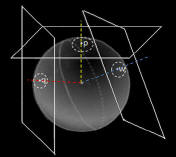
Ya sabemos que
nuestro planeta es esférico. Por simple lógica, toda "cosa", (o mejor hagamos mención a un avión o barco), se encontrará en posición RECTO Y NIVELADO cuando esté en vertical al:
"plano
perpendicular a una línea imaginaria Cuando con nuestra imaginación naveguemos las rutas aquí tratadas, procuremos "ubicar las piezas" en su correcta postura que, si bien parece algo por demás obvio, sin darnos cuenta podemos estar haciéndolo incorrectamente.
El hecho de pensar
que estamos simulando navegaciones en una esfera en donde el "arriba y abajo"
tal vez nos haga girar la cabeza y... |
Por esto, considerar:
|
¿ESTAMOS DE ACUERDO
QUE |
|
|
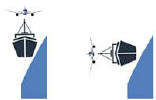
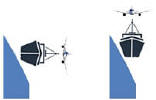
¿ESTAMOS DE ACUERDO QUE |
  |
|
¿ENTONCES COINCIDIMOS QUE SIEMPRE SERÁ DE ESTA MANERA? |

  
|
|
Perfecto!
Todo bien hasta ahí!
Hagamos de cuentas que "mentalmente" estamos analizando un |
 |
Ok.
Comencemos...
En la siguiente
imagen vemos tal cual (como nuestra mente imagina), al paralelo 50.
Notarán, (al igual que lo hace nuestra mente), que se observa totalmente recto.
De hecho, si lo pensamos, el mismo conforma el perímetro de la BASE de un casquete polar que,
cual disco de vinilo, sabemos que es bien recto.
|
|
|
Nuestra mente,
inclusive sin desearlo, ya imagina al barco |
|
|
|
Nos proponemos
navegar por el paralelo 50N, rumbo 090°, |
|
|
|
Visualizamos en
nuestra mente, a nuestro buque ya surcando estas aguas |
|
|
|
Automáticamente, nuestra mente recrea tal
circuito y ubica a nuestro barco circunnavegando el planeta... Pero... Ahora sí vuestra vista (o pensamiento) nos alerta sobre algo! Algo no está bien! Si hemos ubicado a nuestro buque en un lateral del planeta, algo no concuerda con la gravedad de éste. El buque, en su vista lateral, está mal alineado! |
 |
|
Ahora sí! |
|
|
|
Pero no. |
|
|
|
¿Qué pasó? |
Conclusión:
Este, es un mero ejemplo que hecho sobre una navegación por un paralelo, pero
este inconveniente puede ocurrir (reitero: en nuestra mente), ante cualquiera de
estas rutas de las que estamos hablando.
|
Parece una
total tontera de la cual muchos dirán: "Nahhh... Yo, no me equivocaría en eso!"; pero PUEDE PASAR. De hecho, conozco a un instructor náutico de gran currículum quien en charlas en relación a este tipo de rutas, pecaba por confundir estos conceptos terminándole por no CUADRARLE LAS COSAS. |
|
8.- La paradoja.
Luego de haber explicado en su totalidad en cuanto a estos dos tipos de rutas, (aunque dicha explicación fue de carácter NO TÉCNICO/PROFESIONAL) y de haber hecho mención a "la tontería" que figura aquí arriba, AHORA SÍ TOCAREMOS EL TEMA DEL QUE ME ATREVÍ A LLAMAR:
"LA PARADOJA".
Antes de abarcar el tema, es importante en primer instancia definir ciertos conceptos a saber:
|
3.- El término: "NAVEGAR RECTO" no sólo que NO TOMAREMOS en cuenta su actitud vertical en cuanto a su altitud sino que tampoco tendrá relación con poseer "al timón" cien por ciento alineado mecánicamente a la nave, sino que implica que su traza de rumbo ES RECTA en su visión superior (2D); recordando la frase ya dicha "ir para allá" con un dedito apuntando. |
Para ponerlos en
contexto, el hecho que consideré necesario enfocarme en lo que llamé:
"una
paradoja", (no literal), fue por una charla que hemos tenido vía Telegram entre
varios amigos; algunos de ellos pilotos, ingenieros y arquitectos.
Todos éstos, conocedores de este tipo de rutas de una forma u otra; algunos que
las han llevado a cabo en navegación aérea transpolar y otros que al menos
conocen sobre el tema en su aspecto
teórico geográfico/geométrico; aunque esto no implique tener la experiencia de llevarlo a la práctica.
Esta charla, comenzó con una contradicción, "similar a lo dicho en el capitulo anterior", pero ella comenzó por parte de una de las plataformas de uso más común y muy de moda en estos momentos:

Los chats de
"INTELIGENCIA ARTIFICIAL"
Veamos aquí,
algunas capturas de estas plataformas de IA que se han compartido en nuestra
charla vía Telegram:
 |
Aquí vemos, que la respuesta dada por la IA, "ES INCORRECTA"! En relación a todo lo ya dicho en esta Web, ya ha quedado claro que cualquier navegación con rumbos 090° o 270°, SÍ O SÍ se llegará al mismo punto de partida, habiendo circunnavegado por un mismo paralelo y que bajo ningún concepto de llegaría a los polos. |
|
Dejar "quieto
el timón" para seguir recto" y así mantener los grados de rumbo... |
|
|
|
|
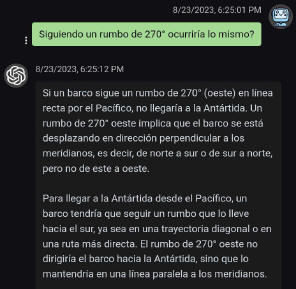 |
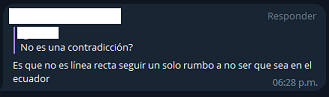
Quien efectuó
la anterior consulta al Chat IA, habiendo identificado su error, replantea
la misma pregunta, pero siendo aún más especifico.
Si bien, la IA
corrige su error anterior, aunque vuelve a equivocarse con eso de "de
norte a sur o de sur a norte". Ya, en su segundo párrafo, lo explica en forma correcta, aunque el temita de "recta" y trayectoria" sigue generando confuciones. |
 |
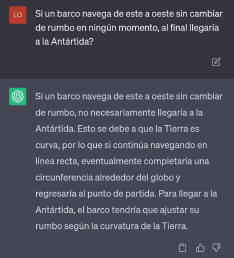
Detectada la contradicción de la IA, (y luego de varios comentarios de los miembros en cuanto a ello), uno de nosotros especifica en nuestra charla, en forma correcta cómo sería esta navegación por sobre un paralelo. |
 |
Un miembro vuelve a consultar
a otro chat IA.
Aquí vemos que el: La IA, continúa su explicación ADENTRÁNDONOS en la PARADOJA mencionada, ya que especifica "navegando en línea recta" a sabiendas que navegar por un paralelo (excluyendo el Ecuador), su traza en vista "superior" será CURVA! He aquí, que comenzamos a confundirnos entre "seguir un rumbo por instrumento" con "poseer el timón alineado mecánicamente con el eje longitudinal de la nave. |
 |
Ufff... Aquí y ante esta respuesta "que fue posterior a las anteriores", es donde nos vuelve a explotar el cerebro!
La IA vuelve a cometer el
mismo error inicial. PERO COMETE UN DOBLE ERROR QUE SERÁ POR DEMÁS DIFÍCIL
NOTARLO dada la paradoja a la que hago mención. Luego y por lógica, complementa su respuesta teórica con sucesos de la práctica; (meteo, corrientes, etc), terminando en su tercer párrafo, reafirmando nuevamente el error .
|
|
|
|
|
Entiéndase, que nuestra charla por Télegram fue mucho más fluida, en donde sólo he hecho capturas de comentarios claves. |
|
|
¿Cómo pretendemos que nuestra mente nos juegue una mala pasada? Analicemos: |
||
 |
 |
 |
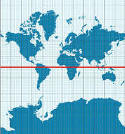
| 1.- Estamos por demás acostumbrados a ver un Mercator con sus paralelos bien rectos. |
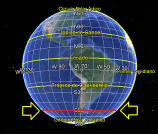
2.- Vemos el globo terráqueo en 2D con paralelos
rectos. (Ojo con ésto. Dependerá del diseño del dibujo, ya que el punto de vista no posee la "dimensión" de la figura a observar). |
3.- Interpretamos que un paralelo divide al planeta en un casquete cuyo paralelo es el perímetro de su "base" que es plana. |
 |
 |
 |
| 4.- Plasmamos una navegación por sobre éstos en forma recta. | 5.- Pero vemos que su traza es curva al igual que lo indica su propia definición. | 6.- Sabemos que para seguir esa ruta "debemos mantener un rumbo" en donde nos "pensamos" que por ello vamos recto. |
|
|
||
|
¿Y pretendemos no confundirnos? |
||
|
Entiéndase, que nuestra charla por Télegram fue mucho más extensa, en donde sólo he hecho capturas de algunos comentarios claves. Vale aclarar que no fue una discusión y/o debate sino que fue una mera y simple charla de carácter por demás escueto. Hasta aquí, todo se enfocaba al error cometido por el mismo chat IA; pero llegó el momento de interpretar en palabras lo que en la práctica se haría al respecto. "Algunos" de los comentarios hechos, son los siguientes: |
|
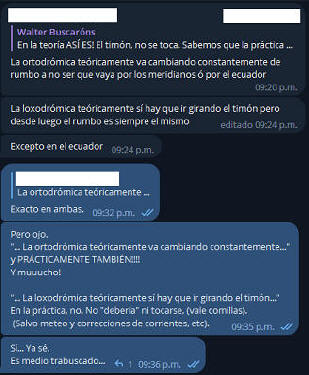 |
Y seguimos adentrándonos
más en LA PARADOJA...
"La ortodrómica
teóricamente va cambiando constantemente de rumbo..." "La loxo teóricamente sí
hay que ir girando el timón pero el rumbo es siempre el mismo"...
MANTENER O NO RUMBO |
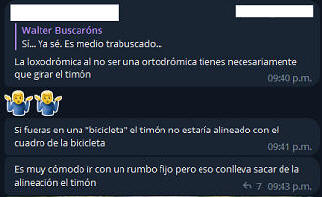 |
Acá "renace" nuevamente la confusión y más cuando se dice literalmente: GIRAR EL TIMÓN Aquí, debemos diferenciar: "MANTENER
EL TIMÓN GIRADO" |
|
Recordando
que en este último cuadro se está hablando de LOXODRÓMICA, ya hemos visto
que por definición es
curva
y que, para mantener EL RUMBO, deberemos mantener el rumbo fijo con el
timón "quieto" pero minúsculamente girado, (imperceptible). Si antes
resultaba confuso, AHORA NOS CONFUNDIMOS MÁS AÚN!... |
|
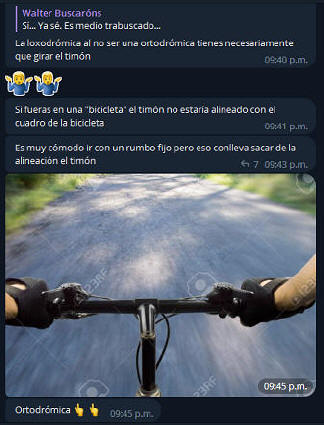 |
He aquí, cuando uno de los integrantes de la charla, gráfica con una
imagen y en forma CORRECTA la ACTITUD REAL del "TIMÓN" ante una
ORTODRÓMICA.. En este caso, en donde tanto timón como rueda, (en el caso de esta bicicleta), se encuentra alineado en 0° al eje longitudinal del vehículo; (creo importante recordar que seguimos ante un ejemplo teórico óptimo, sin clima ni variante alguna).
En cuanto a la brújula que tanto nos interesa, VARIARÁ durante todo su trayecto, (exceptuando sobre el Ecuador y meridianos). |
 |
Aquí, el mismo miembro posteó
una gráfica en forma CORRECTA sobre la ACTITUD REAL del "TIMÓN" ante una
loxodrómica. Deja claro sólo la actitud del timón y no la manipulación en variación de éste, (no daba a la charla), pero identifica que el timón físico no estará alineado al eje longitudinal de la nave. Quien va en bicicleta y dada de la escala que identificaría a este tipo de vehículo, marcaría una clarísima curva en cuanto a trayectoria; pero muy distinto es en navegaciones de gran extensión en nuestro enorme planeta. |
|
La exactitud de esta ruta, estará condicionada a lo preciso que seremos en cuanto al centrado que haremos de ese valor en grados que nos indicará la citada ruta y ni qué hablar de cotejar nuestras coordenadas conforme a nuestra carta de navegación. Pero...
"LOXODRÓMICA: Excepto en el Ecuador y meridianos!" |
|
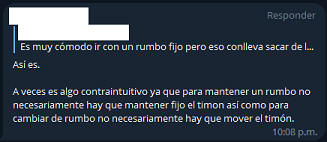 |
En fin. Este último posteo que he capturado de esa sala del chat, creo que resume por completo la comparación entre ambas rutas. Por un lado, que resulta "contraituitivo" (y confuso) y segundo, al no "normalizar" el accionar y la actitud como consecuencia descriptiva al hablar sobre ellas. |
|
|
|
|
Analicemos... |
|||
 |
 |
||
|
Así sería la actitud del timón
ante una |
Así sería la actitud del timón
ante una |
||
|
|
|||
|
EN EL CASO DE ESTA
RUTA |
|||
 |
 |
 |
 |
|
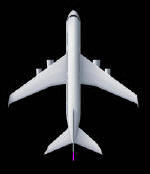
1 Cercano al Ecuador pero con un rumbo superior a los 90°, la inclinación del timón es imperceptible. |
2 A medida que avanza, el descentrado del timón, va en leve aumento. |
3 Sin olvidar que es un ejemplo de visualización exagerada, el timón posee un viraje considerable ante tal ruta. |
4 Ya, cercano al polo, el espiral se va cerrando hasta llegar al mismo. |
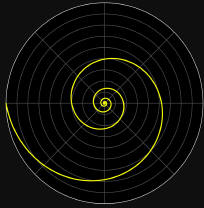
Traza de loxodrómica
en vista superior al polo.
¿Este último ejemplo de ruta loxo
les resulta estúpido y más viendo el comportamiento de su timón?
Claaaro que lo es!
Recuerden que sólo es un ejemplo hipotético NO PRÁCTICO, ya que dicha ruta nace
en el ecuador terrestre y con un rumbo FIJO de apenas un poco menos de 270°!
Nadie, en su sano juicio, efectuaría tan impráctica ruta; pero ejemplos extremos
nos muestra verdades puntuales por más exageradas que estas sean.
|
|
|||
 |
 |
 |
 |
|
1 Cercano al Ecuador (pero no en él) el ángulo del centrado del timón de dirección será por demás ínfimo e imperceptible |
2 Al efectuarlo por paralelos más alejados al Ecuador, el ángulo del centrado del timón de dirección será mayor aunque eso ni implique que sea notorio |
3 Al hacerlo por un paralelo más cercano al polo, mayor aún será el ángulo de centrado mecánico del timón de dirección. |
4 En un hipotético ejemplo "teórico" de volar circunnavegando el polo con un radio a éste ínfimo, lógicamente el ángulo de centrado del timón será por demás notorio como sobrevuela en semicírculo una vertical. |
|
IMPORTANTE ES TIMÓN VIRADO (No confundir con "ir virando el timón") |
|||
Un ejemplo de RUTAS
ORTODRÓMICAS:
Esta es la ruta aérea más corta
desde Santiago de Chile a Ulán Bator en Mongolia. Son unos 18.380km.
Si bien no es una ruta comercial que en la realidad se lleva a cabo, (por falta
de demanda, desde luego), esta sería su traza exacta.
Esta ruta, posee otro gran problema.
Su distancia.
Está al borde de la autonomía máxima de un avión comercial, pudiéndola hacer en
forma muy justa un Airbus A350-900 ULR (Ultra Long Range) o el Boeing 787-9
Dreamliner, el cual el piloto Argentino Enrique Piñeiro logró conseguir con
éste, romper el record de distancia, inclusive superando a la autonomía que, por
default, su fabricante dio para este avión. (Dicho vuelo fue de 19.483
kilómetros, de Seúl a Buenos Aires).
Aquí, visto en un Mercator, la traza de
la ruta
entre Santiago de Chile a Ulán
Bator en Mongolia.
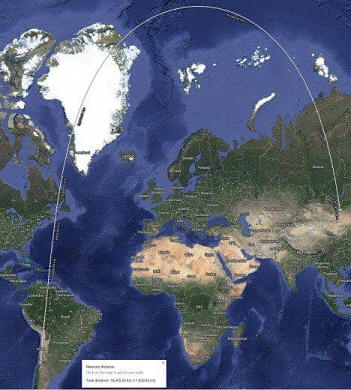
Misma ruta ortodrómica, pero en una
representación esférica.
EL CAMINO MÁS CORTO!

Todo lo escrito en
esta web, es un "hilado fino" hasta tal vez exagerado. (Soy consciente de ello).
A sabiendas que se han excluido muchísimos términos y definiciones por demás
específicos y profesionales, intenté expresarme en un idioma más cotidiano y
entendible.
Soy por demás consciente que, posiblemente quien tenía dudas al respecto, no se
las quitarán con este escrito en una única lectura rápida; debiendo ir y volver
entre párrafo y párrafo.
(Me incluyo en ellos)...
Pero...
Lo importante al caso, es que todo este análisis fino, REALMENTE NO SIRVE PARA
NADA!... Su única función es la de conocer como quien de color de ropa interior
se interesase, sobre aquellos detalles por demás minúsculos y sobre todo "antiprácticos".
Si en lo que en la práctica se refiere, ya sabemos que:
|
|
|
|
|
|
|
Podríamos
detenerlos a trazar dicha ruta sin medios informáticos; pero, seamos
francos; ya estamos en pleno siglo XXI. |
|
10.- Material de terceros.
Sobre este caso y para ampliar más aún sobre estos tipos de rutas, comparto los videos efectuados por mi gran amigo y piloto comercial Marcos Lopez, (X-Avation), quien e forma exquisita explicó sobre ellas en todo su concepto:
|
RUTAS ORTODRÓMICAS Y LOXODRÓMICAS SOLO COMPATIBLES CON UN MUNDO ESFÉRICO |
|||||
|
Analizaremos cuál es el camino más corto en una superficie esférica, llamado ruta Ortodromica, y como estas rutas SOLO Y EXCLUSIVAMENTE se pueden realizar sobre una esfera y veremos cómo comprobamos que realmente los aviones navegan este tipo de rutas, desbancando totalmente cualquier maguferia en relación a otra forma de nuestro planeta. |
|||||
|
RUTAS ETOPS |
|||||
|
¿Por qué en algunos vuelos hay gran diferencia entre la distancia de su ortodromica con respecto a su ruta real? En este video explicaremos la normativa ETOPS y de donde viene. Y veremos cómo su evolución a sido vital para el desarrollo aeronáutico actual. Este tema daría para hablar muchas horas y no profundizare en los conceptos. Mi intención es que tengáis una visión general de las ETOPS. He tratado de ser muy serio y didáctico con el tema. Espero les guste. |
|||||
|
TODOS LOS VUELOS DESTRUYEN EL TERRAPLANISMO - TOP 11 RÉCORDS MUNDIALES |
|||||
|
En este vídeo expondré el top 11 de los récords mundiales de vuelos más largos, y demostraré como todos y cada uno de ellos no tendría ningún sentido en un mundo plano. Todos los vuelos se realizan viajando por las ortodrómicas, y éstas a su vez son una sección de un círculo máximo. Proyectaré ambas figuras geométricas en un mundo plano, para que se vea la diferencia de estas rutas REALES en comparación con la supuesta línea recta de la ruta que se debería realizar en un supuesto mundo plano. |
|||||
|
Nota: La proyección del círculo máximo en el mundo plano que represente es algo más ovalada en la parte que no corresponde a la ortodromica (en la mayoría de los vuelos que trate aqui), pero es difícil dibujarla a mano alzada. La parte que corresponde a la ruta ortodromica si es bastante exacta. |
|||||
|
Todas las rutas reales expuestas en este vídeo son las siguientes, las cuales las podréis introducir en cualquier gestor de planes de vuelo que tengáis, en mi caso uso el Navigraph: Rutas (Hemisferio
Norte) : 11- San Francisco -
Singapur: 10 - Manila - New
York (JFK): 09- Dallas Ft.
Worth - Sydney: 08- Houston- Sidney: 07- Singapur- Los
Ángeles: 06- Dubái- Auckland
(Nueva Zelanda): 05- Perth
(Australia) - Londres: 04 - Auckland
(Nueva Zelanda) - Doha (Qatar): 03- - Newark (Nueva
Yok) a Singapur: 02- Nueva York -
Sidney: 01- Londres Sidney: Rutas (Hemisferio
Sur) : Santiago de Chile
- Sidney: Walvis Bay
(Namibia) - Auckland (Nueva Zelanda): Madagascar - Sidney: |
|||||
|
|
|||||
|
Aquí, algunos videos del
mismo autor, publicados en tik tok: (Se abre en nueva ventana). |
||
 |
 |
 |
| https://vm.tiktok.com/ZMj2cjnGq/ | https://vm.tiktok.com/ZMj2cPWjQ/ | https://vm.tiktok.com/ZMj2cyFH5/ |
"Manual de Navegación Aérea" – OACI
Idioma: Español e inglés
Editorial: Organización de Aviación Civil Internacional (ICAO/OACI)
Contenido: Explica claramente las rutas ortodrómicas como trayectorias sobre círculos máximos. Es un estándar mundial.
"Instrument Flying Handbook" – FAA (FAA-H-8083-15)
Idioma: Inglés
Editorial: Federal Aviation Administration (EE.UU.)
Contenido: Incluye navegación por gran círculo, especialmente en navegación de largo alcance.
"Pilot's Handbook of Aeronautical Knowledge" – FAA (FAA-H-8083-25)
Idioma: Inglés
Contenido: Sección de navegación explica diferencia entre ortodrómica (gran círculo) y loxodrómica.
"Jeppesen Private Pilot Manual" – Jeppesen Sanderson
Idioma: Inglés
Editorial: Jeppesen
Contenido: Sección de navegación aérea general, incluye ortodrómicas en navegación internacional.
"Manual de Navegación Aérea" – Ejército del Aire (España)
Idioma: Español
Editorial: Ministerio de Defensa (España)
Contenido: Muy detallado en geodesia y navegación ortodrómica y loxodrómica.
"Radio Navigation and Instrument Flying" – David Wyatt
Idioma: Inglés
Contenido: Usado en formación EASA ATPL. Trata rutas ortodrómicas y planificación en navegación aérea.
"Manual de Instrucción de Navegación Aérea" – Escuela de Aviación Militar (Argentina)
Idioma: Español
Contenido: Explica geografía aeronáutica, ortodrómica vs. loxodrómica.
Walter Buscaróns
Buenos Aires, Argentina,
Setiembre, 2023